https://distill.pub/
Why Momentum Really Works. The math of gradient descent with momentum.
anon_bwna said in #1857 2y ago:
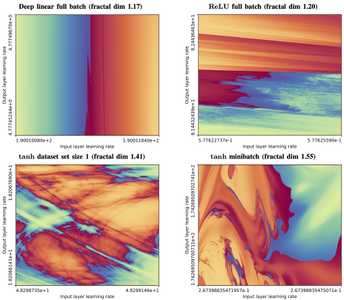
I keep coming back to this classic every time I end up thinking about gradient descent optimizers. Unfortunately we're still left with this pesky "learning rate" parameter that has to be set empirically by what causes convergence vs divergence.
One really interesting thing I saw recently was an illustration that the optimal learning parameters for gradient descent have a fractal boundary. Small perturbations in the problem flip you between convergence/divergence around the boundary in a maximally unsmooth way. This is an elegantly unsurprising result, as the mandelbrot set and other fractals are also the result of a convergence/divergence boundary.
https://sohl-dickstein.github.io/2024/02/12/fractal.html
How does this limit affect adaptive learning rate algorithms that can detect and walk back from divergence? They always seem to have their own parameters that themselves have unprincipled optimal values.
I always wonder where this kind of stuff shows up in for example the human mind. Are some psychological disorders the result of flying too close to the convergence boundary? Obviously the brain isn't fragile to stuff like exploding into NaNs, but surely there's some tuning parameters that can go wrong in weird ways?
One really interesting thing I saw recently was an illustration that the optimal learning parameters for gradient descent have a fractal boundary. Small perturbations in the problem flip you between convergence/divergence around the boundary in a maximally unsmooth way. This is an elegantly unsurprising result, as the mandelbrot set and other fractals are also the result of a convergence/divergence boundary.
https://sohl-dickstein.github.io/2024/02/12/fractal.html
How does this limit affect adaptive learning rate algorithms that can detect and walk back from divergence? They always seem to have their own parameters that themselves have unprincipled optimal values.
I always wonder where this kind of stuff shows up in for example the human mind. Are some psychological disorders the result of flying too close to the convergence boundary? Obviously the brain isn't fragile to stuff like exploding into NaNs, but surely there's some tuning parameters that can go wrong in weird ways?
I keep coming back t
anon_vahy said in #1886 2y ago:
I cannot yet post new threads, but in the same broad space as " sensitivity to empirically determined learning rate parameters", I recently learned about "curriculum learning", in which the particular order of ingest of training data affects model performance: https://arxiv.org/abs/2101.10382
This is in some sense obvious, as different paths through high dimensional space can be radically different given different sequences of steps, but if the effect holds even as the architecture is drowned in data, then it might be a avenue for continued alpha after reaching a scaling plateau.
This is in some sense obvious, as different paths through high dimensional space can be radically different given different sequences of steps, but if the effect holds even as the architecture is drowned in data, then it might be a avenue for continued alpha after reaching a scaling plateau.
I cannot yet post ne
anon_bwna said in #1887 2y ago:
>>1886
Do you know if there is any predictability to the effect? I would guess it's related to catastrophic forgetting aka the reason stochastic gradient descent has to be stochastic. Basically if you update on one set of evidence without locking in those learnings, then update on another, the second clobbers the first. The solution is to digest everything as much as possible with no ordering (interleaved randomly every which way). The other solution is to have a way to lock in learnings in one area so you can learn another without clobbering. I saw a paper on this recently. The catastrophic forgetting effect is an obvious source of path-dependency. It would favor putting the important stuff later, basically equivalent in power to "fine tuning".
There may also be effects in the early stuff getting the model into one valley or another, laying the groundwork of concepts that the rest of the training builds on. I've been wanting to experiment with models that leverage this in the architecture, where you add more parameters after the basics have been established in some more limited but real domain.
Do you know if there is any predictability to the effect? I would guess it's related to catastrophic forgetting aka the reason stochastic gradient descent has to be stochastic. Basically if you update on one set of evidence without locking in those learnings, then update on another, the second clobbers the first. The solution is to digest everything as much as possible with no ordering (interleaved randomly every which way). The other solution is to have a way to lock in learnings in one area so you can learn another without clobbering. I saw a paper on this recently. The catastrophic forgetting effect is an obvious source of path-dependency. It would favor putting the important stuff later, basically equivalent in power to "fine tuning".
There may also be effects in the early stuff getting the model into one valley or another, laying the groundwork of concepts that the rest of the training builds on. I've been wanting to experiment with models that leverage this in the architecture, where you add more parameters after the basics have been established in some more limited but real domain.
Do you know if there